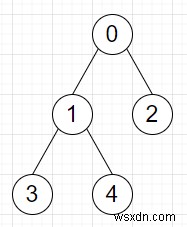
ধরুন আমাদের [u, v] আকারে গাছের প্রান্তগুলির একটি তালিকা আছে, এটি নির্দেশ করে যে u এবং v এর মধ্যে একটি অনির্দেশিত প্রান্ত রয়েছে। এবং আমাদের দুটি মানও আছে x এবং y। যদি আমরা নোড x এ থাকি এবং আমাদের প্রতিপক্ষ y নোডে থাকে। প্রথম রাউন্ডে, আমরা সরে যাই, তারপর পরের রাউন্ডে প্রতিপক্ষের নড়াচড়া ইত্যাদি। প্রতিপক্ষ একটি রাউন্ডে একটি পদক্ষেপ না করতে নির্বাচন করতে পারে। প্রতিপক্ষকে ধরতে আমাদের ন্যূনতম রাউন্ডের সংখ্যা খুঁজে বের করতে হবে।
সুতরাং, যদি ইনপুট হয় edges =[[0, 1], [0, 2], [1, 3], [1, 4]], x =0, y =3, তাহলে আউটপুট হবে 3, প্রথমে যেমন, আমরা নোড 0 থেকে 1 এ চলে যাই। তারপরে প্রতিপক্ষ বর্তমান নোড 3-তে থাকে। তারপর আমরা নোড 3-এ চলে যাই।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
N :=1^5 + 5
-
পরিদর্শন করা আকারের একটি অ্যারে সংজ্ঞায়িত করুন:N এবং আরেকটি অ্যারে পরিদর্শন করা 2 আকারের:N তাদের −1 দিয়ে পূরণ করুন
-
N নোডের জন্য সংলগ্ন তালিকা গ্রাফ তৈরি করুন
-
প্রতিটি প্রান্তের জন্য এটি প্রান্ত তালিকায়, করুন
-
গ্রাফ[it[u]]
এর শেষে এটি [v] সন্নিবেশ করুন -
গ্রাফ[it[v]]
এর শেষে এটি[u] ঢোকান
-
-
একটি সারি সংজ্ঞায়িত করুন w
-
q
-এ ঢোকান -
পরিদর্শন করেছেন [u] :=0
-
q খালি না থাকলেও −
করুন-
নোড :=q এর প্রথম উপাদান
-
q
থেকে উপাদান মুছুন -
প্রতিটি নোডের জন্য এটি গ্রাফ[নোড]
এ-
যদি পরিদর্শন করা হয় [এটি] −1 এর সমান, তাহলে −
-
পরিদর্শন করেছে [এটি] :=পরিদর্শন করেছে [নোড] + 1
-
এটি q
-এ ঢোকান
-
-
-
-
q
-এ v সন্নিবেশ করান -
ret :=0
-
পরিদর্শন 2[v] :=0
-
যখন q খালি নয়), −
করুন-
নোড :=q এর প্রথম উপাদান
-
q
থেকে উপাদান মুছুন -
ret :=সর্বাধিক ret এবং 2 * (পরিদর্শন করা হয়েছে[নোড])
-
প্রতিটি নোডের জন্য এটি গ্রাফ[নোড]
এ-
যদি পরিদর্শন 2[এটি] -1 এবং পরিদর্শন 2[নোড] + 2 <পরিদর্শন করা[এটি] এর মতো হয়, তাহলে −
-
visited2[it] :=visited2[node] + 1
-
এটি q
-এ ঢোকান
-
-
-
-
রিটার্ন রিটার্ন
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int visited[N];
int visited2[N];
vector<int> graph[N];
class Solution {
public:
int solve(vector<vector<int>>& edges, int u, int v) {
memset(visited, −1, sizeof visited);
memset(visited2, −1, sizeof visited2);
for (int i = 0; i < N; i++)
graph[i].clear();
for (auto& it : edges) {
graph[it[0]].push_back(it[1]);
graph[it[1]].push_back(it[0]);
}
queue<int> q;
q.push(u);
visited[u] = 0;
while (!q.empty()) {
int node = q.front();
q.pop();
for (auto& it : graph[node]) {
if (visited[it] == −1) {
visited[it] = visited[node] + 1;
q.push(it);
}
}
}
q.push(v);
int ret = 0;
visited2[v] = 0;
while (!q.empty()) {
int node = q.front();
q.pop();
ret = max(ret, 2 * (visited[node]) − 1);
for (auto& it : graph[node]) {
if (visited2[it] == −1 && visited2[node] + 2 <
visited[it]) {
visited2[it] = visited2[node] + 1;
q.push(it);
}
}
}
return ret;
}
};
int solve(vector<vector<int>>& edges, int u, int v) {
return (new Solution())−>solve(edges, u, v);
}
int main(){
vector<vector<int>> edge = {{0, 1},{0, 2},{1, 3},{1, 4}};
int x = 0, y = 3;
cout << solve(edge, x, y);
} ইনপুট
[ [0, 1], [0, 2], [1, 3], [1, 4] ], 0, 3
আউটপুট
3


