ধরুন আমাদের দুটি আকার আছে, ডমিনো এবং ট্রোমিনো৷ ডোমিনো 2 x 1 আকৃতির এবং ট্রোমিনোগুলি 'L' আকৃতির মতো। তাদের নিচের মত ঘোরানো যেতে পারে −
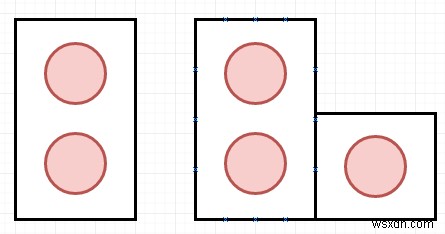
যদি আমাদের একটি সংখ্যা n থাকে, তাহলে এই দুই ধরনের টুকরা দিয়ে একটি 2 x n বোর্ড পূরণ করার জন্য আমাদের কনফিগারেশনের সংখ্যা খুঁজে বের করতে হবে। আমরা টাইলিংয়ের ক্ষেত্রে জানি, প্রতিটি বর্গক্ষেত্র একটি টালি দ্বারা আবৃত করা আবশ্যক।
সুতরাং যদি ইনপুট 3 হয়, তাহলে আউটপুট হবে 5। সুতরাং বিন্যাসগুলি [XYZ XXZ XYY XXY XYY] এবং [XYZ YYZ XZZ XYY XXY] হতে পারে, এখানে বিভিন্ন টাইলের জন্য বিভিন্ন অক্ষর ব্যবহার করা হয়েছে।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
N + 5 আকারের dp নামে একটি অ্যারে তৈরি করুন, সেট করুন dp[1] :=1, dp[2] :=2 এবং dp[3] :=5
-
আমি রেঞ্জ 4 থেকে N
এর জন্য-
dp[i] :=2*dp[i − 1] + dp[i − 3]
-
-
dp[N>
ফেরত দিন
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7;
int add(int a, int b){
return ((a % MOD) + (b % MOD)) % MOD;
}
class Solution {
public:
int solve(int N) {
vector <int> dp(N + 5);
dp[1] = 1;
dp[2] = 2;
dp[3] = 5;
for(int i = 4; i <= N; i++){
dp[i] = add(2 * dp[i − 1], dp[i − 3]);
}
return dp[N];
}
};
main(){
Solution ob;
cout << (ob.solve(3));
} ইনপুট
3
আউটপুট
5


