এর নোডগুলির ওজন সহ একটি বাইনারি গাছ দেওয়া হয়েছে৷ লক্ষ্য হল নোডের সংখ্যা খুঁজে বের করা যার ওজন আছে যাতে সংখ্যাটি একটি নিখুঁত বর্গ। যদি ওজন 36 হয় তবে এটি 62 হয় তাই এই নোডটি গণনা করা হবে।
উদাহরণস্বরূপ
ইনপুট
মান ইনপুট করার পরে যে গাছটি তৈরি হবে তা নীচে দেওয়া হল -
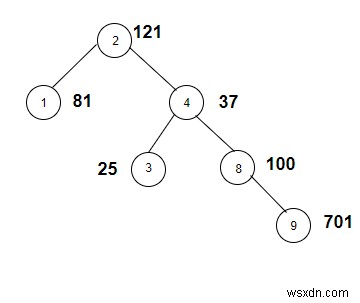
আউটপুট
Count the nodes whose weight is a perfect square are: 4
ব্যাখ্যা
আমাদের ট্রি নোড এবং প্রতিটি নোডের সাথে সম্পর্কিত ওজন দেওয়া হয়। এখন আমরা পরীক্ষা করি যে নোডের সংখ্যাগুলি নিখুঁত বর্গ কিনা৷
| নোড | ওজন | পারফেক্ট বর্গ | হ্যাঁ/না |
|---|---|---|---|
| 2 | 121 | 11*11 | হ্যাঁ |
| 1 | 81 | 9*9 | হ্যাঁ |
| 4 | 37 | প্রধান সংখ্যা | না |
| 3 | 25 | 5*5 | হ্যাঁ |
| 8 | 100 | 10*10 | হ্যাঁ |
| 9 | 701 | সম্ভব নয় | না |
ইনপুট
মান ইনপুট করার পরে যে গাছটি তৈরি হবে তা নীচে দেওয়া হল -
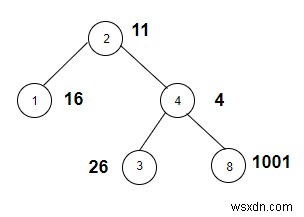
আউটপুট
Count the nodes whose weight is a perfect square are: 2
ব্যাখ্যা
we are given with the tree nodes and the weights associated with each node. Now we check whether the digits of nodes are perfect squares or not.
| নোড | ওজন | পারফেক্ট বর্গ | হ্যাঁ / না |
|---|---|---|---|
| 2 | 11 | সম্ভব নয় | না |
| 1 | 16 | 4*4 | হ্যাঁ |
| 4 | 4 | 2*2 | হ্যাঁ |
| 3 | 26 | সম্ভব নয় | না |
| 8 | 1001 | সম্ভব নয় | না |
নিম্নলিখিত প্রোগ্রামে ব্যবহৃত পদ্ধতি −
এই পদ্ধতিতে আমরা গাছের গ্রাফে ডিএফএস প্রয়োগ করব যাতে এটি অতিক্রম করা যায় এবং নোডের ওজন একটি নিখুঁত বর্গ কিনা তা পরীক্ষা করে দেখব। এই উদ্দেশ্যে দুটি ভেক্টর Node_Weight(100) এবং edge_graph[100] নিন।
-
নোডের ওজন দিয়ে নোড_ওয়েট[] শুরু করুন।
-
ভেক্টর এজ_গ্রাফ ব্যবহার করে একটি গাছ তৈরি করুন।
-
একটি গ্লোবাল ভেরিয়েবল বর্গ নিন এবং এটি 0 দিয়ে শুরু করুন।
-
ফাংশন চেক(int check_it) একটি পূর্ণসংখ্যা নেয় এবং check_it একটি নিখুঁত বর্গ হলে সত্য ফেরত দেয়।
-
মোট =sqrt(check_it)
নিন -
এখন যদি(floor(total) !=ceil(total)) সত্য হয় তাহলে মোট একটি নিখুঁত বর্গ নয়, মিথ্যা ফেরত দেয়।
-
অন্যথায় সত্য ফেরত দিন।
-
ফাংশন perfect_square(int নোড, int root) একটি গাছের একটি নোড এবং রুট নোড নেয় এবং প্রদত্ত গাছে নোডের সংখ্যা ফেরত দেয় যার ওজন একটি নিখুঁত বর্গ।
-
যদি (চেক(নোড_ওজন[নোড])) সত্য হয়, তাহলে বর্গ বৃদ্ধি করুন।
-
লুপের জন্য ব্যবহার করে ভেক্টর এজ_গ্রাফ[নোড] এ ট্র্যাভার্স ট্রি।
-
ভেক্টরের পরবর্তী নোডের জন্য perfect_square(it, node) কল করুন।
-
সমস্ত ফাংশনের শেষে আমাদের কাছে নোডের সংখ্যা হিসাবে একটি বর্গ থাকবে যার ওজন একটি নিখুঁত বর্গ হিসাবে মান থাকবে৷
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
vector<int> Node_Weight(100);
vector<int> edge_graph[100];
int square = 0;
bool check(int check_it){
double total = sqrt(check_it);
if(floor(total) != ceil(total)){
return false;
}
return true;
}
void perfect_square(int node, int root){
if(check(Node_Weight[node])){
square++;
}
for (int it : edge_graph[node]){
if(it == root){
continue;
}
perfect_square(it, node);
}
}
int main(){
//weight of the nodes
Node_Weight[2] = 121;
Node_Weight[1] = 81;
Node_Weight[4] = 37;
Node_Weight[3] = 25;
Node_Weight[8] = 100;
Node_Weight[9] = 701;
//create graph edge
edge_graph[2].push_back(1);
edge_graph[2].push_back(4);
edge_graph[4].push_back(3);
edge_graph[4].push_back(8);
edge_graph[8].push_back(9);
perfect_square(2, 2);
cout<<"Count the nodes whose weight is a perfect square are: "<<square;
return 0;
} আউটপুট
যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট −
উৎপন্ন করবেCount the nodes whose weight is a perfect square are: 4


