L ={0m1(n+m)2n | এর জন্য পুশডাউন অটোমেটা তৈরি করুন C++ এ m,n =0}

আমাদের একটি ভাষা "L" দেওয়া হয়েছে এবং কাজটি হল প্রদত্ত ভাষার জন্য একটি পুশডাউন অটোমেটা তৈরি করা যা ব্যাখ্যা করে যে 1 এর সংঘটন 0 এবং 2 এর সংঘটনের সংযোজন হবে এবং এছাড়াও, 0 এবং 2 এর উপস্থিতি ন্যূনতম একটি হবে যা স্ট্রিংটিকে NULLও করতে পারে এবং এটি স্বয়ংক্রিয়ভাবে গ্রহণ করা উচিত৷

পুশডাউন অটোমেটা কি?

একটি পুশডাউন অটোমেটা বা পুশডাউন অটোমেটন বা পিডিএ হল একটি প্রসঙ্গ-মুক্ত ব্যাকরণ প্রয়োগ করার একটি কৌশল যেভাবে আমরা একটি নিয়মিত ব্যাকরণের জন্য ডিটারমিনিস্টিক ফিনিট অটোমেটন বা ডিএফএ ডিজাইন করি। একটি ডিএফএ সীমিত ডেটাতে কাজ করতে পারে, কিন্তু একটি পিডিএ অসীম ডেটাতে কাজ করতে পারে। আমরা পুশডাউন অটোমেটা বুঝতে পারি "সীমাবদ্ধ স্টেটমেশিন" এবং একটি "স্ট্যাক" এর সংমিশ্রণ হিসেবে।

একটি পুশডাউন অটোমেটনের তিনটি উপাদান থাকে -

• একটি ইনপুট টেপ,

• একটি নিয়ন্ত্রণ ইউনিট, এবং

• অসীম আকারের একটি স্ট্যাক।

একটি PDA আনুষ্ঠানিকভাবে 7-টুপল হিসাবে বর্ণনা করা যেতে পারে (Q, Σ, S, δ, q0, I, F) −

• Q হল রাজ্যের সসীম সংখ্যা

• Σ হল ইনপুট বর্ণমালা

• S হল স্ট্যাক চিহ্ন

• δ হল ট্রানজিশন ফাংশন:Q × (Σ υ {ε}) × S × Q × S*

• q0 হল প্রাথমিক অবস্থা (q0 Ε Q)

• I হল প্রাথমিক স্ট্যাক টপ চিহ্ন (I Ε S)

• F হল গ্রহণযোগ্য অবস্থার একটি সেট (F Ε Q)

আসুন প্রদত্ত ভাষার জন্য একটি পুশডাউন অটোমেটা তৈরি করি −

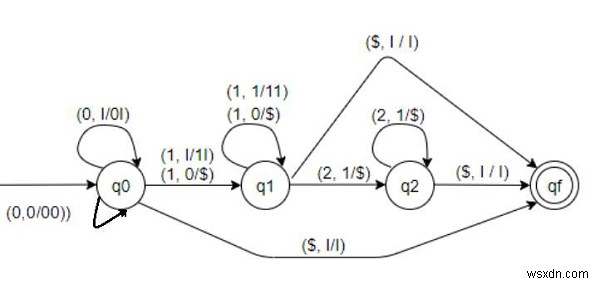
এই PDA দ্বারা গ্রহণযোগ্য স্ট্রিংগুলি হল −

• 0 ^m 1 ^m − 01, 0011, 000111 ইত্যাদি। 0 এর সংখ্যা সংখ্যার সমান। 1s. যখন n 0 হবে তখন আমাদের কোন 2s থাকবে না। 0s চাপতে থাকুন এবং প্রথম 1 এর সম্মুখীন হওয়ার সাথে সাথে 0s পপ করুন। যদি আমরা স্ট্রিংয়ের শেষে পৌঁছাই এবং 0 সেকেন্ড ছাড়াই স্ট্রিংটি গৃহীত হয়।

• 1 ⁿ 2 ⁿ − 12, 1122, 111222 ইত্যাদি। 1s এর সংখ্যা সংখ্যার সমান। 2s. যখন m 0 হবে তখন আমাদের কোন 0s থাকবে না। 1s পুশ করতে থাকুন এবং প্রথম 2 এর সম্মুখীন হওয়ার সাথে সাথে পপ 1s। যদি আমরা স্ট্রিং এর শেষে পৌছাই এবং কোন 1s না থাকে তাহলে স্ট্রিংটি গৃহীত হবে৷

• 0 ⁿ 1 ^m+n 2 ^m − 0112, 001112, 001112 ইত্যাদি। 1s এর সংখ্যা সংখ্যার যোগফলের সমান। 0 এবং 2 সেকেন্ডের। প্রথম 1 এর সম্মুখীন হওয়ার সাথে সাথে 0s চাপতে থাকুন তারপর 0s বাকি না হওয়া পর্যন্ত 0s পপ করুন। এখন আবার 1s চাপুন যতক্ষণ না প্রথম 2 সম্মুখীন হয়। তারপর প্রতিটি 2 এর জন্য 1s পপিং করা শুরু করুন যতক্ষণ না আমাদের কাছে 1s নেই। যদি আমরা শেষ পর্যন্ত পৌঁছাই এবং কোন 1 বাকি না থাকে তাহলে স্ট্রিংটি গৃহীত হবে।

• NULL স্ট্রিংও গৃহীত হয়। 0 ⁰ 1 ⁰ 2 ⁰

আসুন মেশিনটি বুঝুন

• অবস্থা q0 −

  এর জন্য রূপান্তর

  • ( 0, I/0I ) − যদি স্ট্যাকের শীর্ষ I হয় এবং বর্তমান ইনপুট প্রতীক 0 হয় তাহলে স্ট্যাকের শীর্ষে 0 ধাক্কা দিন এবং q0 এ থাকুন। স্ট্যাক হয়ে যায় 0I...

  • ( 0, 0/00 ) − যদি স্ট্যাকের শীর্ষ 0 হয় এবং বর্তমান ইনপুট প্রতীকটিও 0 হয় তবে স্ট্যাকের শীর্ষে 0 ধাক্কা দিন এবং q0 এ থাকুন। স্ট্যাক 00 হয়ে যায়.... পরবর্তী 1 বা 2 পর্যন্ত 0s চাপতে থাকুন।

  • ( 1, I/1I ) − যদি স্ট্যাকের উপরে I হয় এবং বর্তমান ইনপুট প্রতীক 1 হয় তাহলে স্ট্যাকের উপরে 1 ধাক্কা দিন এবং q1 এ যান। স্ট্যাক হয়ে যায় 1I...

  • ( 1, 0/$ ) − যদি স্ট্যাকের শীর্ষ 0 হয় এবং বর্তমান ইনপুট প্রতীক 1 হয় তাহলে 0 পপ করুন এবং q1 এ যান৷

  • ( 1, 0/$ ) − যদি স্ট্যাকের শীর্ষ 0 হয় এবং বর্তমান ইনপুট প্রতীক 1 হয় তাহলে 0 পপ করুন এবং q1 এ যান৷

• অবস্থা q1 −

  এর জন্য রূপান্তর

  • ( 1, 1/11 ) − যদি স্ট্যাকের শীর্ষ 1 হয় এবং বর্তমান ইনপুট চিহ্নটিও 1 হয় তবে স্ট্যাকের শীর্ষে 1 টিপুন এবং q1 এ থাকুন। স্ট্যাক 11 হয়ে যায়.... পরবর্তী 0 বা 2 পর্যন্ত 1s পুশ করতে থাকুন।

  • ( 1, 0/$ ) − যদি স্ট্যাকের শীর্ষ 0 হয় এবং বর্তমান ইনপুট প্রতীক 1 হয় তাহলে 0 পপ করুন এবং q1 এ থাকবেন।

  • ( $, I/I ) − যদি স্ট্যাকের শীর্ষে I হয় এবং কোনো ইনপুট না থাকে তাহলে কিছুই করবেন না এবং qf এ যান৷

  • ( 2, 1/$ ) − যদি স্ট্যাকের শীর্ষ 1 হয় এবং বর্তমান ইনপুট প্রতীক 2 হয় তাহলে 1 পপ করুন এবং q2 এ যান৷

• q2 −

  অবস্থার জন্য রূপান্তর

  • ( 2, 1/$ ) − যদি স্ট্যাকের শীর্ষ 1 হয় এবং বর্তমান ইনপুট প্রতীক 2 হয় তাহলে 1 পপ করুন এবং q2 তে থাকবে।

  • ( $, I/I ) − যদি স্ট্যাকের শীর্ষে I হয় এবং কোনো ইনপুট না থাকে তাহলে কিছুই করবেন না এবং qf এ যান৷