এই সমস্যায়, আমাদের দুটি মান দেওয়া হয়েছে k1 এবং k2 (k1
সমস্যা বর্ণনা: আমরা ক্রমবর্ধমান ক্রমে n1 থেকে n2 পর্যন্ত গাছের সমস্ত কী প্রিন্ট করব।
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট:
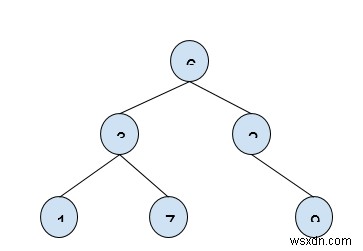
k1 =4, k2 =12
আউটপুট: ৬, ৭, ৯
সমাধান পদ্ধতি
সহজ আমরা ইনঅর্ডার ট্রাভার্সাল ব্যবহার করে সমস্যার সমাধান করতে পারি কিন্তু স্থান জটিলতা 0(n) আছে কিন্তু সময়ের প্রয়োজন হল O(1) জটিলতায় সমাধান করা। সুতরাং, এর জন্য, আমরা একটি বিশেষ ধরনের ট্রাভার্সাল কৌশল ব্যবহার করব।
আমরা মরিস ট্রাভার্সাল ব্যবহার করব যা থ্রেডেড বাইনারি গাছের উপর ভিত্তি করে। এটির কোনো স্ট্যাক/সারি প্রয়োজন হয় না এবং তথ্য সঞ্চয় করতে NULL পয়েন্টার ব্যবহার করে, এটি স্টোরেজকে O(1) এ কমাতে সাহায্য করে।
সমস্যা সমাধানের জন্য মরিস ট্রাভার্সালের কাজ চিত্রিত করার জন্য প্রোগ্রাম,
উদাহরণ
#include <iostream>
using namespace std;
struct node {
int data;
struct node *left, *right;
};
node* insertNode(int data) {
node* temp = new node;
temp->data = data;
temp->right = temp->left = NULL;
return temp;
}
void RangeTraversal(node* root, int k1, int k2) {
if (!root)
return;
node* nodeTraversal = root;
while (nodeTraversal) {
if (nodeTraversal->left == NULL) {
if (nodeTraversal->data <= k2 && nodeTraversal->data >= k1)
cout<<nodeTraversal->data<<" ";
nodeTraversal = nodeTraversal->right;
}
else {
node* prevNode = nodeTraversal->left;
while (prevNode->right != NULL && prevNode->right != nodeTraversal)
prevNode = prevNode->right;
if (prevNode->right == NULL) {
prevNode->right = nodeTraversal;
nodeTraversal = nodeTraversal->left;
}
else {
prevNode->right = NULL;
if (nodeTraversal->data <= k2 && nodeTraversal->data >= k1)
cout<<nodeTraversal->data<<" ";
nodeTraversal = nodeTraversal->right;
}
}
}
}
int main() {
node* root = insertNode(6);
root->left = insertNode(3);
root->right = insertNode(2);
root->left->left = insertNode(1);
root->left->right = insertNode(7);
root->right->right = insertNode(9);
cout<<"All BST keys in the given range are \t";
RangeTraversal(root, 4, 10);
return 0;
} আউটপুট
All BST keys in the given range are 7 6 9


