ভার্টেক্স কভার সমস্যা

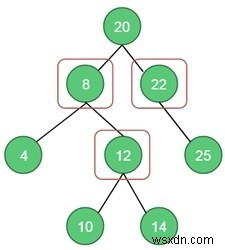
একটি অনির্দেশিত গ্রাফের জন্য, শীর্ষবিন্দু কভারটি শীর্ষবিন্দুগুলির একটি উপসেট, যেখানে গ্রাফের প্রতিটি প্রান্তের (u, v) জন্য হয় u বা v সেটে থাকে৷

একটি বাইনারি ট্রি ব্যবহার করে, আমরা সহজেই ভার্টেক্স কভার সমস্যা সমাধান করতে পারি।

এই সমস্যাটিকে দুটি উপ-সমস্যায় ভাগ করা যায়। যখন মূলটি শীর্ষবিন্দু কভারের অংশ। এই ক্ষেত্রে, রুট সমস্ত শিশুদের প্রান্ত জুড়ে। আমরা সহজভাবে বাম এবং ডান উপ-বৃক্ষের জন্য শীর্ষবিন্দু কভারের আকার খুঁজে পেতে পারি এবং মূলের জন্য 1 যোগ করতে পারি।

ইনপুট এবং আউটপুট

Input:
A binary tree.
Output:
The vertex cover is 3.
 

অ্যালগরিদম

vertexCover(root node)

এই সমস্যায়, একটি বাইনারি ট্রি গঠিত হবে, প্রতিটি নোড সেই নোড দ্বারা আচ্ছাদিত ডেটা এবং শীর্ষবিন্দুর সংখ্যা ধারণ করবে৷

ইনপুট - বাইনারি গাছের মূল।

আউটপুট - মূল দ্বারা আচ্ছাদিত শীর্ষবিন্দুর সংখ্যা৷

Begin
   if root is φ, then
      return 0
   if root has no child, then
      return 0
   if vCover(root) ≠ 0, then
      return vCover(root)
   withRoot := 1 + vertexCover(left(root)) + vertexCover(right(root))
   withoutRoot := 0

   if root has left child, then
      withoutRoot := withoutRoot + vertexCover(left(left(root))) + vertexCover(left(right(root)))
   if root has right child, then
      withoutRoot := withoutRoot + vertexCover(right(left(root))) + vertexCover(right(right(root)))
   return vCover(root)
End

উদাহরণ

#include <iostream>
#include <algorithm>
using namespace std;

struct node {
   int data;
   int vCover;
   node *left, *right;
};

node *getNode(int data) {
   node *newNode = new (node);
   newNode->data = data;
   newNode->vCover = 0; //set vertex cover to 0
   newNode->left = NULL;
   newNode->right = NULL;
   return newNode;    //newly created node
}

int vertexCover(node *root) {
   if(root == NULL)    //when tree is empty
      return 0;
   if(root->left == NULL && root->right == NULL)    //when no other edge from root
      return 0;
         
   if(root->vCover != 0)   //when vertex cover of this node is found, leave that node
      return root->vCover;
         
   int sizeWithRoot = 1 + vertexCover(root->left) + vertexCover(root->right);
   int sizeWithOutRoot = 0;
   
   if(root->left != NULL)   //when root is not included and go for left child
      sizeWithOutRoot += 1 + vertexCover(root->left->left) + vertexCover(root->left->right);
   if(root->right != NULL)    //when root is not included and go for right child
      sizeWithOutRoot += 1 + vertexCover(root->right->left) + vertexCover(root->right->right);
   
   root->vCover = (sizeWithRoot < sizeWithOutRoot)?sizeWithRoot:sizeWithOutRoot; //minimum vertex cover
   return root->vCover;
}

int main() {
   //create tree to check vertex cover
   node *root = getNode(20);
   root->left = getNode(8); root->right = getNode(22);
   root->left->left = getNode(4); root->left->right = getNode(12);
   root->left->right->left = getNode(10); root->left->right->right = getNode(14);
   root->right->right = getNode(25);
   cout << "Minimal vertex cover: " << vertexCover(root);
}

আউটপুট

Minimal vertex cover: 3