পাইথন প্রোগ্রামে একটি সংখ্যার অনন্য মৌলিক গুণনীয়কের গুণফল

এই নিবন্ধে, আমরা নীচে দেওয়া সমস্যার বিবৃতিটির সমাধান সম্পর্কে শিখব −

সমস্যা বিবৃতি

একটি সংখ্যা n দেওয়া হলে, আমাদের উপলব্ধ সমস্ত অনন্য মৌলিক গুণনীয়কের গুণফল খুঁজে বের করতে হবে এবং তা ফেরত দিতে হবে।

উদাহরণস্বরূপ

Input: num = 11
Output: Product is 11

ব্যাখ্যা

এখানে, ইনপুট সংখ্যা হল 11 যার শুধুমাত্র 1 মৌলিক গুণনীয়ক রয়েছে এবং এটি 11। তাই তাদের গুণফল হল 11।

পন্থা 1

i =2 থেকে n+1 পর্যন্ত লুপ ব্যবহার করে i n-এর একটি ফ্যাক্টর কিনা এবং তারপরে পরীক্ষা করুন যে আমি নিজেই মৌলিক সংখ্যা কিনা, যদি হ্যাঁ তাহলে পণ্য ভেরিয়েবলে পণ্য সংরক্ষণ করুন এবং i =n না হওয়া পর্যন্ত এই প্রক্রিয়াটি চালিয়ে যান।

উদাহরণ

def productPrimeFactors(n):
   product = 1
   for i in range(2, n+1):
      if (n % i == 0):
         isPrime = 1
         for j in range(2, int(i/2 + 1)):
            if (i % j == 0):
               isPrime = 0
               break
      if (isPrime):
         product = product * i
   return product
# main
n = 18
print (productPrimeFactors(n))

আউটপুট

120

সমস্ত ভেরিয়েবলের সুযোগ নীচের ছবিতে দেখানো হয়েছে −

পন্থা 2

1) যখন n 2 দ্বারা বিভাজ্য (এমনকি), প্রিন্ট 2 এবং n কে 2 দ্বারা ভাগ করুন।

2) ধাপ 1 এর পরে, n অবশ্যই বিজোড় হয়ে যাবে। এখন i =3 থেকে n এর বর্গমূল পর্যন্ত একটি ফর লুপ শুরু করুন। যখন আমি n ভাগ করে, প্রিন্ট i এবং i দ্বারা n ভাগ করে। আমি n ভাগ করতে ব্যর্থ হওয়ার পরে, i 2 দ্বারা বৃদ্ধি করুন এবং প্রক্রিয়াটি চালিয়ে যান।

3) যদি n একটি মৌলিক সংখ্যা হয় এবং 2 এর বেশি হয়, তাহলে উপরের দুটি ধাপে n 1 হবে না। তাই n প্রিন্ট করুন যদি এটি 2 এর বেশি হয়।

উদাহরণ

import math
def productPrimeFactors(n):
   product = 1
   # prime factor 2
   if (n % 2 == 0):
      product *= 2
      while (n%2 == 0):
         n = n/2
   # n must be odd
   for i in range (3, int(math.sqrt(n)), 2):
      # While i divides n, print i and
      # divide n
      if (n % i == 0):
         product = product * i
         while (n%i == 0):
            n = n/i
   # n is a prime number greater than 2
   if (n > 2):
      product = product * n
   return product
# main()
n = 8
print (int(productPrimeFactors(n)))

আউটপুট

2

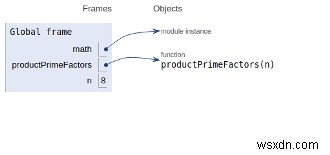
ভেরিয়েবলের স্কোপ নিচের ছবিতে উল্লেখ করা হয়েছে −

উপসংহার

এই প্রবন্ধে, আমরা একটি ব্রুট ফোর্স এপ্রোচ এবং একটি দক্ষ পন্থা সহ একটি প্রদত্ত সংখ্যার অনন্য মৌলিক ফ্যাক্টরগুলির গুণফল সম্পর্কে শিখেছি