প্রদত্ত পরিসরে বিজোড় ফ্যাক্টর সহ উপাদানের সংখ্যার জন্য পাইথন প্রোগ্রাম

এই নিবন্ধে, আমরা নীচে দেওয়া সমস্যার বিবৃতিটির সমাধান সম্পর্কে জানব৷

সমস্যা বিবৃতি − আমাদের একটি পরিসর দেওয়া হয়েছে, আমাদের পরিসরে বিজোড় কারণের সংখ্যা খুঁজে বের করতে হবে।

পন্থা

আমরা সবাই জানি যে সমস্ত নিখুঁত বর্গক্ষেত্রে একটি পরিসরে বিজোড় সংখ্যক ফ্যাক্টর থাকে। তাই এখানে আমরা অনেকগুলো নিখুঁত বর্গ গণনা করব।

যেহেতু m এবং n উভয়ই অন্তর্ভুক্ত, তাই n একটি নিখুঁত বর্গ হওয়ার ক্ষেত্রে ত্রুটি এড়াতে আমরা সূত্রে n-1 নিই।

এখন আসুন নীচের বাস্তবায়ন দেখি-

উদাহরণ

# count function
def count(n, m):
   return int(m**0.5) - int((n-1)**0.5)
# main
n = 25
m = 400
print("Number of odd squares are: ", count(n, m))

আউটপুট

Number of odd squares are: 16

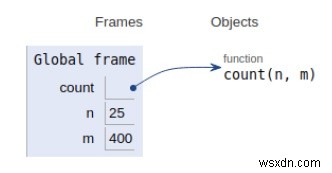
উপরের চিত্রে দেখানো হিসাবে সমস্ত ভেরিয়েবল এবং ফাংশন গ্লোবাল স্কোপে ঘোষণা করা হয়েছে।

উপসংহার

এই নিবন্ধে, আমরা শিখেছি কিভাবে আমরা একটি নির্দিষ্ট পরিসরে বিজোড় ফ্যাক্টর সহ উপাদানের সংখ্যা খুঁজে পেতে পারি।