পাইথনে একটি পরিবর্তিত চেসবোর্ডে যখন N রাত থাকে তখন রাজা একটি বৈধ পদক্ষেপ নিতে পারে কিনা তা পরীক্ষা করে দেখুন

ধরুন আমাদের দাবার মতো একই নিয়মের সাথে একটি অসীম দাবাবোর্ড আছে এবং যদি অসীম দাবাবোর্ডে এবং রাজার স্থানাঙ্কে N নাইট স্থানাঙ্ক থাকে, তাহলে রাজা চেকমেট কিনা তা আমাদের পরীক্ষা করতে হবে। অসীম বোর্ডের স্থানাঙ্ক বৃহৎ মান দ্বারা আবদ্ধ যেমন (-10^9 <=x, y <=10^9)।

সুতরাং, যদি ইনপুট হয় নাইট পজিশন =[[2,1],[1,3],[3,6],[5,5],[6,1],[7,3]] এবং রাজার অবস্থান :[৪,৩],

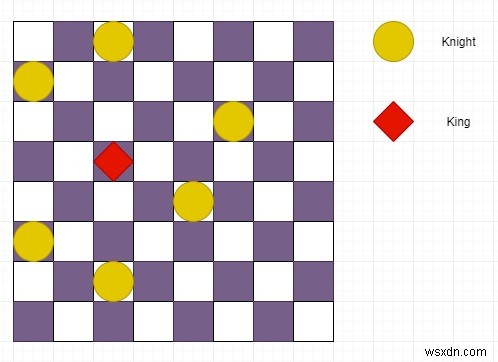
তাহলে আউটপুট হবে True, যেহেতু রাজার কোন চাল নেই, তাই এটি চেক মেট।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• my_dict :=একটি নতুন মানচিত্র
• আমি 0 থেকে n রেঞ্জের জন্য, কর
  • x :=a[i, 0]
  • y :=a[i, 1]
  • my_dict[x, y] :=1
  • my_dict[x - 2, y + 1] :=1
  • আমার_ডিক্ট[x - 2, y - 1] :=1
  • my_dict[x + 1, y + 2] :=1
  • my_dict[x + 1, y - 2] :=1
  • my_dict[x - 1, y + 2] :=1
  • my_dict[x + 2, y + 1] :=1
  • my_dict[x + 2, y - 1] :=1
  • আমার_ডিক্ট[x - 1, y - 2] :=1
-1 থেকে 1 রেঞ্জের মধ্যে
• এর জন্য, করুন
  • -1 থেকে 1 পর্যন্ত j-এর জন্য, করুন
    • nx :=king_pos[0] + i
    • ny :=king_pos[1] + j
    • যদি i 0 এর মত না হয় এবং j 0 এর মত না হয়, তাহলে
      • যদি my_dict[(nx, ny)] শূন্য হয়, তাহলে
        • মিথ্যে ফেরত দিন
• সত্য ফেরান

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def is_checkmate(a, n, king_pos):my_dict ={} সীমার মধ্যে i এর জন্য(0, n):x =a[i][0] y =a[i][1] my_dict[(x, y)] =1 আমার_ডিক্ট[(x - 2, y + 1)] =1 আমার_ডিক্ট[(x - 2, y - 1)] =1 আমার_ডিক্ট[(x + 1, y + 2)] =1 আমার_ডিক্ট[( x + 1, y - 2)] =1 my_dict[(x - 1, y + 2)] =1 my_dict[(x + 2, y + 1)] =1 my_dict[(x + 2, y - 1) ] =1 my_dict[(x - 1, y - 2)] =1 রেঞ্জে i এর জন্য(-1, 2):j এর জন্য রেঞ্জ(-1, 2):nx =king_pos[0] + i ny =king_pos [1] + j if i !=0 এবং j !=0:যদি না হয় my_dict[(nx, ny)]:রিটার্ন False return Truea =[[2,1],[1,3],[3,6] ,[5,5],[6,1],[7,3]]n =len(a)pos =[4, 3]প্রিন্ট (is_checkmate(a, n, pos))

ইনপুট

আউটপুট

সত্য