ধরুন আমাদের কাছে একটি সংলগ্ন তালিকা উপস্থাপনা হিসাবে একটি গ্রাফ আছে, আমাদের 2D ম্যাট্রিক্স M খুঁজে বের করতে হবে যেখানে
-
M[i, j] =1 যখন শীর্ষবিন্দু i এবং j এর মধ্যে একটি পথ থাকে।
-
M[i, j] =0 অন্যথায়।
সুতরাং, যদি ইনপুট মত হয়
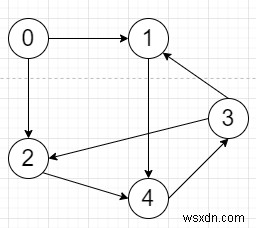
তাহলে আউটপুট হবে
| 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
উত্তর:=n x n আকারের একটি 2d ম্যাট্রিক্স, যেখানে n হল শীর্ষবিন্দুর সংখ্যা, 0s দিয়ে পূরণ করুন
-
0 থেকে n রেঞ্জের জন্য, করুন
-
q:=একটি সারি, এবং প্রথমে i ঢোকান
-
q খালি না থাকার সময়, করুন
-
node:=q এর প্রথম উপাদান, এবং q
থেকে প্রথম উপাদান মুছে দিন -
যদি ans[i, node] অ-শূন্য হয়, তাহলে
-
পরবর্তী পুনরাবৃত্তির জন্য যান
-
-
ans[i, node]:=1
-
প্রতিবেশী:=গ্রাফ[নোড]
-
প্রতিটি n প্রতিবেশীর জন্য, করুন
-
q
এর শেষে n সন্নিবেশ করান
-
-
-
-
উত্তর ফেরত দিন
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
উদাহরণ
শ্রেণির সমাধান:def solve(self, graph):ans=[[0 for _ graph] for _ in graph] for i in range(len(graph)):q=[i] যখন q:node=q.pop(0) if ans[i][node]:চালিয়ে যান ans[i][node]=1 পড়শী=গ্রাফ[নোড] প্রতিবেশীদের মধ্যে n এর জন্য:q.append(n) ফেরত আনসব =সমাধান()adj_list =[[1,2],[4],[4],[1,2],[3]]priunt(ob.solve(adj_list))
ইনপুট
[[1,2],[4],[4],[1,2],[3]]


