পাইথনে মার্জ করার পরে ন্যূনতম সংখ্যার রঙগুলি খুঁজে বের করার প্রোগ্রামটি থাকে

ধরুন আমাদের কাছে রঙের একটি তালিকা আছে (R, G, B)। এখন যদি দুটি ভিন্ন রঙ একে অপরের পাশে থাকে তবে তারা তৃতীয় রঙের একক রঙের আইটেমে রূপান্তরিত হতে পারে। এই ধরনের রূপান্তরের যেকোন সম্ভাব্য ক্রমানুসারে আমাদের অবশিষ্ট ক্ষুদ্রতম সংখ্যা খুঁজে বের করতে হবে।

সুতরাং, যদি ইনপুটটি রঙের মত হয় =["G", "R", "G", "B", "R"], তাহলে আউটপুট হবে 1 কারণ এটি নীচের মত রূপান্তর করতে পারে −

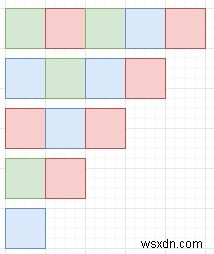
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• n :=রঙের আকার
• যদি রঙের শুধুমাত্র একটি স্বতন্ত্র রঙ থাকে, তাহলে
  • রিটার্ন n
• যদি n <=1 হয়, তাহলে
  • রিটার্ন n
• x :=0
• d :=মূল মান জোড়া সহ একটি মানচিত্র {("R", 1), ("G", 2), ("B", 3)}
• রঙের প্রতিটি c-এর জন্য, করুন
  • x :=x XOR d[c]
• 2 রিটার্ন করুন যদি x 0 এর মত হয় অন্যথায় 1

উদাহরণ (পাইথন)

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

class Solution:
   def solve(self, colors):
      n = len(colors)
      if len(set(colors)) == 1:
         return n
      if n <= 1:
         return n
      x = 0
      d = {"R": 1, "G": 2, "B": 3}
      for qux in colors:
         x ^= d[qux]
      return 2 if x == 0 else 1   
ob = Solution()
colors = ["G", "R", "G", "B", "R"]
print(ob.solve(colors))

ইনপুট

["G", "R", "G", "B", "R"]

আউটপুট

1