পাইথনে DFA ব্যবহার করে 3-এর বাইনারি স্ট্রিং মাল্টিপল আছে কিনা তা পরীক্ষা করুন

ধরুন আমাদের একটি অ্যারে n আছে যা যেকোনো সংখ্যার একটি বাইনারি প্রতিনিধিত্ব করে। ডিটারমিনিস্টিক ফিনিট অটোমেটা ডিএফএ ব্যবহার করে আমাদের এটির বাইনারি উপস্থাপনা তিন দ্বারা বিভাজ্য কিনা তা পরীক্ষা করতে হবে৷

সুতরাং, যদি ইনপুটটি n =[1, 1, 0, 0] (12-এর বাইনারি) এর মত হয়, তাহলে আউটপুট হবে True।

এটি সমাধান করার জন্য, আমরা নীচের মত DFA তৈরি করতে পারি −

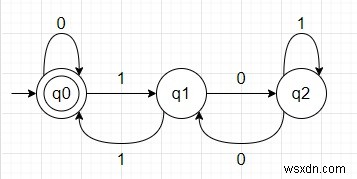
পদ্ধতিটি সহজ যখন একটি সংখ্যা 3 দ্বারা বিভাজ্য হয় তখন অবশিষ্টাংশ 0 হবে, যদি না হয় তাহলে অবশিষ্টাংশ 1 বা 2 হবে। এই তিনটি অবশিষ্টাংশের জন্য তিনটি অবস্থা রয়েছে। প্রারম্ভিক অবস্থাও চূড়ান্ত অবস্থা কারণ যখন অবশিষ্টাংশ 0 হয় তার মানে সংখ্যাটি বিভাজ্য।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• dfa_state :=0
• আমি 0 থেকে সংখ্যার আকার - 1 এর রেঞ্জের জন্য, কর
  • সংখ্যা :=সংখ্যা[i]
  • যদি dfa_state 0 হয়, তাহলে
    • অঙ্ক যদি 1 এর মত হয়, তাহলে
      • dfa_state :=1
  • অন্যথায় যখন dfa_state 1 হয়, তারপর
    • অঙ্ক যদি 0 এর মত হয়, তাহলে
      • dfa_state :=2
    • অন্যথায়,
      • dfa_state :=0
  • অন্যথায় যখন dfa_state 2 হয়, তারপর
    • অঙ্ক যদি 0 এর মত হয়, তাহলে
      • dfa_state :=1
• যদি dfa_state 0 হয়, তাহলে
  • সত্য ফেরান
• মিথ্যে ফেরত দিন

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

def solve(nums):
   dfa_state = 0
   for i in range(len(nums)):
      digit = nums[i]
      if dfa_state == 0:
         if digit == 1:
            dfa_state = 1
         elif dfa_state == 1:
            if digit == 0:
               dfa_state = 2
            else:
               dfa_state = 0
         elif dfa_state == 2:
            if digit == 0:
               dfa_state = 1
            if dfa_state == 0:
               return True
   return False
n = [1, 1, 0, 0]
print(solve(n))

ইনপুট

[1, 1, 0, 0]

আউটপুট

True