পাইথনে ভেক্টর এ ঘুরিয়ে এবং ভেক্টর সি যোগ করে ভেক্টর বি-তে পৌঁছানো সম্ভব কিনা তা পরীক্ষা করুন

ধরুন আমাদের 2D সমতলে x, y এবং z তিনটি ভেক্টর আছে। 90 ডিগ্রী (ঘড়ির কাঁটার দিকে) ঘোরার মাধ্যমে বা প্রয়োজনে যতবার এটির সাথে z যোগ করে আমরা ভেক্টর x থেকে ভেক্টর y পেতে পারি কিনা তা পরীক্ষা করতে হবে।

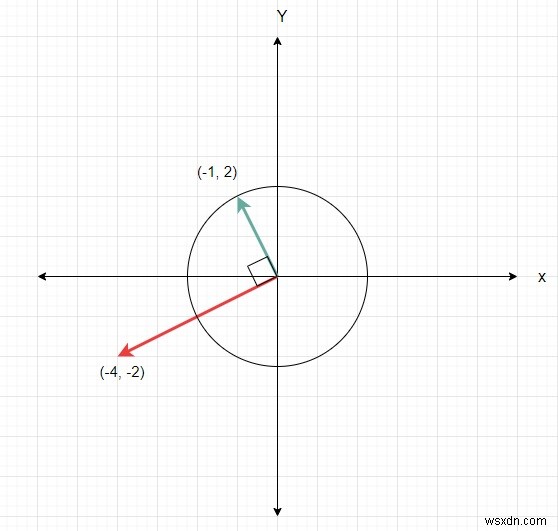
সুতরাং, যদি ইনপুটটি x =(-4, -2) y =(-1, 2) z =(-2, -1) এর মত হয় তবে আউটপুটটি True হবে কারণ আমরা অবস্থান পেতে x এর সাথে z যোগ করতে পারি। (-2, -1), তারপর (-1, 2) পেতে 90° ঘড়ির কাঁটার দিকে ঘোরান।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

একটি ফাংশন util() সংজ্ঞায়িত করুন। এটি p, q, r, s

• d :=r * r + s * s
• যদি d 0 এর সমান হয়, তাহলে
  • যখন p এবং q উভয়ই 0 হয় তখন সত্য ফেরত দিন, অন্যথায় মিথ্যা
• সত্য প্রত্যাবর্তন করুন যখন (p * r + q * s) এবং (q * r - p * s) উভয়ই d দ্বারা বিভাজ্য, অন্যথায় মিথ্যা
• প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -
• যদি util(p এর x - q এর x, q এর p - y এর q, r এর x, r এর y) অথবা util(p এর x + q এর x, p + q এর y) এর যে কোনো একটি 1], r এর x, r এর y) বা util(p এর x - q এর y, p এর y + q এর x, r এর x, r এর y) বা util(p এর x + q এর y, y p - q এর x, r এর x, r এর y) সত্য, তাহলে
  • সত্য ফেরান
• মিথ্যে ফেরত দিন

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def util(p, q, r, s):
   d = r * r + s * s
   if d == 0:
      return p == 0 and q == 0
   return (p * r + q * s) % d == 0 and (q * r - p * s) % d == 0
def solve(p,q,r):
   if util(p[0] - q[0], p[1] - q[1], r[0], r[1]) or util(p[0] + q[0], p[1] + q[1], r[0], r[1]) or util(p[0] - q[1], p[1] + q[0], r[0], r[1]) or util(p[0] + q[1], p[1] - q[0], r[0], r[1]):
      return True
   return False
p = (-4, -2)
q = (-1, 2)
r = (-2, -1)
print(solve(p, q, r))

ইনপুট

(-4, -2), (-1, 2), (-2, -1)

আউটপুট

True