ধরুন আমাদের দুটি অ্যারে আছে nums1 এবং nums2। একটি বৈধ পথকে নিম্নরূপ সংজ্ঞায়িত করা হয়েছে -
-
অতিক্রম করতে nums1 বা nums2 নির্বাচন করুন (সূচী-0 থেকে)।
-
বাম থেকে ডানে অ্যারে অতিক্রম করুন৷
এখন, যদি আমরা nums1 এবং nums2-এ উপস্থিত যেকোন মানের মধ্য দিয়ে যাচ্ছি তাহলে আমরা অন্য অ্যারের পাথ পরিবর্তন করতে পারি। এখানে স্কোর হল একটি বৈধ পথে অনন্য মানের সমষ্টি। আমাদের সম্ভাব্য সব বৈধ পথের সর্বোচ্চ স্কোর খুঁজে বের করতে হবে। যদি উত্তরটি খুব বড় হয় তাহলে ফলাফল মডিউল 10^9+7।
সুতরাং, যদি ইনপুট nums1 =[3,5,6,9,11] nums2 =[5,7,9,10] এর মত হয়, তাহলে আউটপুট হবে 35 কারণ −
-
সংখ্যা 1 থেকে শুরু হওয়া বৈধ পথগুলি হল:[3,5,6,9,11], [3,5,6,9,10], [3,5,7,9,10], [3,5,7, 9,11]
-
সংখ্যা2 থেকে শুরু হওয়া বৈধ পথগুলি হল:[5,7,9,10], [5,6,9,11], [5,6,9,10], [5,7,9,11]
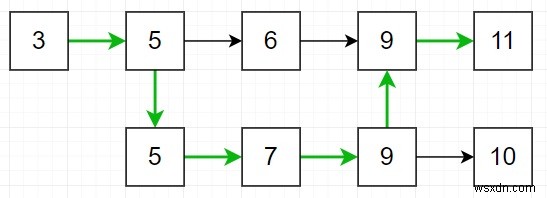
সুতরাং সর্বাধিক [3,5,7,9,11]।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
M :=সংখ্যা 1 এর আকার , N :=সংখ্যা 2 এর আকার
-
যোগফল1 :=0, যোগফল2 :=0
-
i :=0, j :=0
-
res :=0
-
যখন i
-
যদি nums1[i]
-
যোগফল1 :=যোগফল1 + সংখ্যা1[i]
-
i :=i + 1
-
-
অন্যথায় যখন nums1[i]> nums2[j], তারপর
-
যোগফল2 :=যোগফল2 + সংখ্যা2[j]
-
j :=j + 1
-
-
অন্যথায়,
-
res :=res + sum1 এর সর্বোচ্চ, (sum2 + nums1[i])
-
i :=i + 1
-
j :=j + 1
-
যোগফল1 :=0
-
যোগফল2 :=0
-
-
-
যখন আমি
-
যোগফল1 :=যোগফল1 + সংখ্যা1[i]
-
i :=i + 1
-
-
যখন j
-
যোগফল2 :=যোগফল2 + সংখ্যা2[j]
-
j :=j + 1
-
-
রিটার্ন (res + sum1 এর সর্বোচ্চ, sum2) mod 10^9+7
উদাহরণ
আসুন আরও ভালভাবে বোঝার জন্য নিম্নলিখিত বাস্তবায়ন দেখি
def solve(nums1, nums2):
M, N = len(nums1), len(nums2)
sum1, sum2 = 0, 0
i, j = 0, 0
res = 0
while i < M and j < N:
if nums1[i] < nums2[j]:
sum1 += nums1[i]
i += 1
elif nums1[i] > nums2[j]:
sum2 += nums2[j]
j += 1
else:
res += max(sum1, sum2) + nums1[i]
i += 1
j += 1
sum1 = 0
sum2 = 0
while i < M:
sum1 += nums1[i]
i += 1
while j < N:
sum2 += nums2[j]
j += 1
return (res + max(sum1, sum2)) % 1000000007
nums1 = [3,5,6,9,11]
nums2 = [5,7,9,10]
print(solve(nums1, nums2)) ইনপুট
[3,5,6,9,11], [5,7,9,10]
আউটপুট
35


