পাইথনে প্রান্ত দৈর্ঘ্য সীমিত পথের অস্তিত্ব পরীক্ষা করার জন্য প্রোগ্রাম

ধরুন আমাদের একটি এজলিস্ট ব্যবহার করে n নোড সহ একটি আনডিরেক্টেড ওয়েটেড গ্রাফ আছে, যেখানে edgeList[i] এর তিনটি প্যারামিটার রয়েছে (u, v, w) বোঝায় যে u থেকে v পর্যন্ত একটি পথ রয়েছে যার দূরত্ব হল w। আমাদের আরেকটি ক্যোয়ারী অ্যারে আছে যেখানে query[i] আছে (p, q, lim)। এই প্রশ্নটি জিজ্ঞাসা করার চেষ্টা করছে যে p থেকে q পর্যন্ত একটি পথ (সরাসরি বা অন্য কোনো নোডের মাধ্যমে) আছে কিনা যার দূরত্ব লিমের চেয়ে কম। আমাদের প্রতিটি প্রশ্নের জন্য সত্য/মিথ্যা ফলাফল ধারণ করে একটি অ্যারে ফেরত দিতে হবে।

সুতরাং, যদি ইনপুট মত হয়

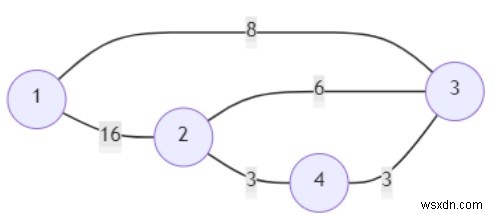
তাহলে আউটপুট হবে [True, False, True]। কারণ 1 থেকে 4 পর্যন্ত যেতে আমরা 1 -> 3 -> 4 11 খরচ সহ পথ অনুসরণ করতে পারি, দ্বিতীয়টি মিথ্যা কারণ আমরা 3 এর কম ব্যবহার করে 2 থেকে 3 পর্যন্ত যেতে পারি না এবং শেষটি সত্য কারণ আমরা 1 থেকে যেতে পারি পাথ 1 -> 3 -> 2 ব্যবহার করে 14 খরচ সহ 2 থেকে যা 15 এর কম৷

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• অভিভাবক :=0 থেকে n পর্যন্ত একটি তালিকা

• rank :=n+1 আকারের একটি তালিকা এবং 0

  দিয়ে পূরণ করুন

• একটি ফাংশন সংজ্ঞায়িত করুন find()। এটি অভিভাবক, x

  লাগবে

• যদি অভিভাবক[x] x এর মতো হয়, তাহলে

  • রিটার্ন x

• পিতামাতা[x] :=খুঁজুন(পিতামাতা, পিতামাতা[x])

• ফেরত অভিভাবক[x]

• একটি ফাংশন ইউনিয়ন () সংজ্ঞায়িত করুন। এটি অভিভাবক, a, b

  লাগবে

• a :=খুঁজুন(পিতামাতা, ক)

• b :=খুঁজুন(পিতা-মাতা, খ)

• a যদি b এর মত হয়, তাহলে

  • ফেরত

• যদি র‍্যাঙ্ক[a]

  • পিতামাতা[a] :=b

• অন্যথায় যখন rank[a]> rank[b], তারপর

  • পিতামাতা[b] :=a

• অন্যথায়,

  • পিতামাতা[b] :=a

  • rank[a] :=rank[a] + 1

• প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -

• ওজন পরামিতির উপর ভিত্তি করে এজলিস্ট সাজান

• res :=প্রশ্নের সংখ্যা সহ একটি অ্যারে এবং 0 দিয়ে পূরণ করুন

• প্রশ্ন :=প্রতিটি সূচক i এর জন্য জোড়ার একটি তালিকা (i, ch) এবং প্রশ্ন থেকে ch মান

• সীমা প্যারামিটারের উপর ভিত্তি করে প্রশ্নগুলি সাজান

• ind :=0

• প্রতিটি সূচকের জন্য আমি প্রশ্নে ট্রিপলেট (a, b, w) করি, করুন

  • যখন ind

    • ইউনিয়ন(অভিভাবক, এজলিস্ট[ইন্ড, 0])

    • ind :=ind + 1

  • res[i] :=find(parent, a) find(parent, b)

    এর মতই

• রিটার্ন রিটার্ন

উদাহরণ

আসুন আরও ভালভাবে বোঝার জন্য নিম্নলিখিত বাস্তবায়ন দেখি

def solve(n, edgeList, queries):
   parent = [i for i in range(n+1)]

   rank = [0 for i in range(n+1)]

   def find(parent, x):

      if parent[x] == x:
         return x
      parent[x] = find(parent, parent[x])
      return parent[x]

   def union(parent, a, b):

      a = find(parent, a)
      b = find(parent, b)

      if a == b:
         return

      if rank[a] < rank[b]:
         parent[a] = b
      elif rank[a] > rank[b]:
         parent[b] = a
      else:
         parent[b] = a
         rank[a] += 1

   edgeList.sort(key = lambda x: x[2])
   res = [0] * len(queries)
   queries = [[i, ch] for i, ch in enumerate(queries)]
   queries.sort(key = lambda x: x[1][2])

   ind = 0
   for i, (a, b, w) in queries:

      while ind < len(edgeList) and edgeList[ind][2] < w:
         union(parent, edgeList[ind][0], edgeList[ind][1])
         ind += 1

      res[i] = find(parent, a) == find(parent, b)
   return res

n = 4
edgeList = [(1,2,16),(1,3,8),(2,4,3),(2,3,6),(4,3,3),]
queries = [(1,4,12),(2,3,3),(1,2,15)]
print(solve(n, edgeList, queries))

ইনপুট

4, [(1,2,16),(1,3,8),(2,4,3),(2,3,6),(4,3,3)],[(1,4,12),(2,3,3),(1,2,15)]

আউটপুট

[True, False, True]