পাইথনে সর্বোচ্চ বিল্ডিং উচ্চতা খুঁজে বের করার প্রোগ্রাম

ধরুন আমাদের একটি মান n এবং জোড়ার আরেকটি তালিকা আছে যাকে সীমাবদ্ধতা বলা হয়। আমরা একটি শহরে নতুন ভবন নির্মাণ করতে চাই। কিন্তু কিছু বিধিনিষেধ আছে। আমরা একটি লাইনে তৈরি করতে পারি এবং ভবনগুলিকে 1 থেকে n পর্যন্ত লেবেল করা হয়। বিধিনিষেধের দুটি প্যারামিটার আছে, তাই সীমাবদ্ধতা[i] =(id_i, max_height_i) নির্দেশ করে id_i-এর উচ্চতা max_height_i এর থেকে কম বা সমান হতে হবে। নতুন ভবনগুলির উচ্চতার উপর শহরের সীমাবদ্ধতাগুলি নিম্নরূপ -

• প্রতিটি বিল্ডিংয়ের উচ্চতা অবশ্যই 0 বা ধনাত্মক মান হতে হবে।

• প্রথম বিল্ডিং উচ্চতা 0 হতে হবে.

• যেকোনো দুটি সংলগ্ন ভবনের উচ্চতার মধ্যে পার্থক্য 1 এর বেশি হতে পারে না।

আমাদের সবচেয়ে উঁচু ভবনের সর্বোচ্চ সম্ভাব্য উচ্চতা খুঁজে বের করতে হবে।

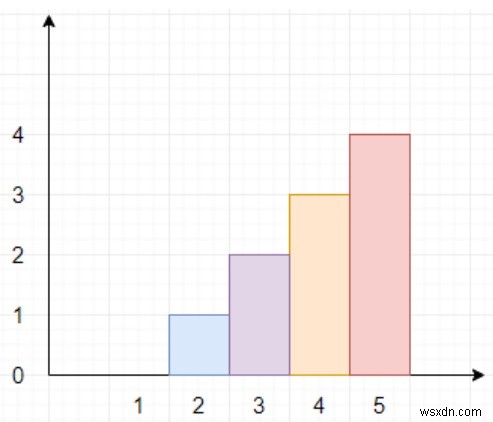
সুতরাং, যদি ইনপুটটি n =5, সীমাবদ্ধতা =[[2,1], [4,3]] এর মত হয়, তাহলে আউটপুট হবে 4 কারণ আমাদের সর্বোচ্চ সম্ভাব্য উচ্চতা খুঁজে বের করতে হবে, তাই এটি 4 হতে পারে যেমন দেখানো হয়েছে ডায়াগ্রাম।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• যদি সীমাবদ্ধতা খালি হয়, তাহলে

  • রিটার্ন n-1

• resi :=আইডির উপর ভিত্তি করে তালিকার সীমাবদ্ধতাগুলি সাজান

• k :=0

• idx :=1

• প্রতিটি resi এর জন্য, করুন

  • re[1] :=সর্বনিম্ন re[1] এবং (k+re[0]-idx)

  • k :=পুনরায়[1]

  • idx :=re[0]

• k :=রেসিতে শেষ উপাদানের সর্বোচ্চ উচ্চতা

• idx :=resi এ শেষ উপাদানের id

• তালিকাটি উল্টো করুন

• প্রথম আইটেম থেকে পরবর্তী প্রতিটির জন্য, করুন

  • re[1] :=সর্বনিম্ন re[1] এবং (k-re[0]+idx)

  • k :=পুনরায়[1]

  • idx :=re[0]

• তালিকাটি উল্টো করুন

• f :=0

• idx :=1

• res :=0

• প্রতিটি resi এর জন্য, করুন

  • ff :=সর্বনিম্ন (f+re[0]-idx) এবং re[1]

  • res :=res এর সর্বোচ্চ এবং ভাগফল (re[0] - idx + f + ff)/2

  • idx :=re[0]

  • f :=ff

• সর্বোচ্চ (f+n-idx) এবং res

  ফেরত দিন

উদাহরণ

আসুন আরও ভালভাবে বোঝার জন্য নিম্নলিখিত বাস্তবায়ন দেখি

def solve(n, restrictions):
   if not restrictions:
      return n-1
   resi = sorted(restrictions, key = lambda x:x[0])

   k = 0
   idx = 1
   for re in resi:
      re[1] = min(re[1], k+re[0]-idx)
      k = re[1]
      idx = re[0]
   k = resi[-1][1]
   idx = resi[-1][0]
   resi.reverse()
   for re in resi[1:]:
      re[1] = min(re[1], k-re[0]+idx)
      k = re[1]
      idx = re[0]
   resi.reverse()

   f = 0
   idx = 1
   res = 0
   for re in resi:
      ff = min(f+re[0]-idx, re[1])
      res = max(res, (re[0] - idx + f + ff) // 2)
      idx = re[0]
      f = ff
   return max(f+n-idx,res)

n = 5
restrictions = [[2,1],[4,3]]
print(solve(n, restrictions))

ইনপুট

5, [[2,1],[4,3]]

আউটপুট

4