ধরুন আমাদের একটি তালিকায় কার্টেসিয়ান পয়েন্টের একটি সেট আছে যাকে পয়েন্ট বলা হয়। আমাদের তাদের মেরু কোণের উপর ভিত্তি করে সাজাতে হবে। মেরু কোণ 0 এবং 2*PI পরিসরে পরিবর্তিত হয়। যদি কিছু বিন্দুতে একই মেরু কোণ থাকে, তাহলে উত্স থেকে সেই বিন্দুর দূরত্বের উপর ভিত্তি করে সেগুলিকে সাজান৷
সুতরাং, যদি ইনপুট পয়েন্টের মত হয় =[(1,1), (1,-2), (-2,2), (5,4), (4,5), (2,3), (- 3,4)],
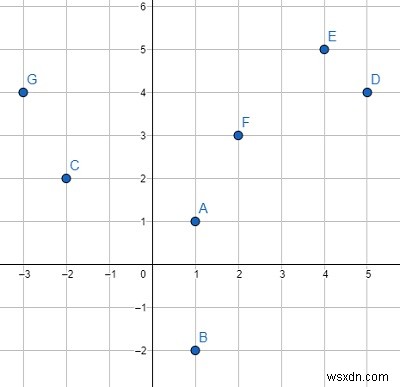
তাহলে আউটপুট হবে [(5, 4), (1, 1), (4, 5), (2, 3), (-3, 4), (-2, 2), (1, -2) ]
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
- একটি তুলনাকারী ফাংশন কী() সংজ্ঞায়িত করুন। এটি x লাগবে
- atan :=x[1]/x[0] এর ট্যান-বিপরীত
- রিটার্ন পেয়ার (atan, x[1]^2+x[0]^2) যদি atan>=0 অন্যথায় (2*pi + atan, x[0]^2+x[1]^2)<
- তারপর তুলনাকারী ফাংশন কী() ব্যবহার করে পয়েন্ট বাছাই করুন
উদাহরণ
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
ম্যাথডেফ সমাধান(পয়েন্ট) আমদানি করুন:ডিএফ কী(এক্স):atan =math.atan2(x[1], x[0]) রিটার্ন (atan, x[1]**2+x[0]** 2) যদি atan>=0 অন্য (2*math.pi + atan, x[0]**2+x[1]**2) রিটার্ন সাজানো (পয়েন্ট, কী=কী) পয়েন্ট =[(1,1) , (1,-2),(-2,2),(5,4),(4,5),(2,3),(-3,4)]প্রিন্ট(সল্ভ(পয়েন্ট))
ইনপুট
[(1,1), (1,-2), (-2,2), (5,4), (4,5), (2,3), (-3,4)]আউটপুট
[(5, 4), (1, 1), (4, 5), (2, 3), (-3, 4), (-2, 2), (1, -2)]


