প্রদত্ত অ্যারে সাজানোর জন্য সংঘটিত বিপর্যয়ের গণনাকে বিপরীত গণনা বলা হয়। ইনভার্সন সমস্যা হল একটি ক্লাসিক্যাল সমস্যা যা মার্জ সর্ট অ্যালগরিদম ব্যবহার করে সমাধান করা যেতে পারে। এই সমস্যা v এ আমরা তার থেকে বাম দিকে সমস্ত উপাদান গণনা করব এবং আউটপুটে গণনা যোগ করব। এই লজিকটি মার্জ সর্টের মার্জ ফাংশনের ভিতরে করা হয়।
বিষয়টি ভালোভাবে বোঝার জন্য একটি উদাহরণ দেওয়া যাক। আসুন আমরা মার্জ প্রক্রিয়ার সাথে জড়িত দুটি সাব-অ্যারে বিবেচনা করি -



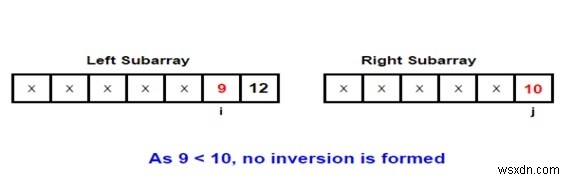
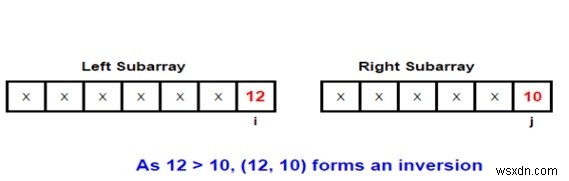
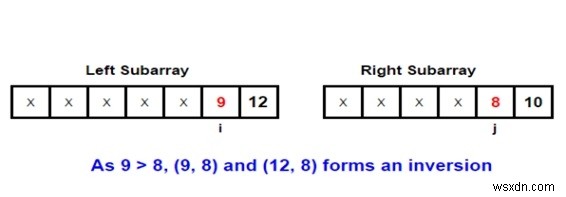
Input: arr[] = { 1, 9, 6, 4, 5}
Output: Inversion count is 5 ব্যাখ্যা
একটি অ্যারের বিপরীত সংখ্যা
একটি অ্যারে দেওয়া, এটির বিপরীত সংখ্যা খুঁজুন। যদি (i
উদাহরণস্বরূপ,
অ্যারেতে 5টি ইনভার্সশন আছে
(9,6), (9,4), (9,5), (6,4), (6,5)
1. উপাদানের মান একে অপরের সাথে তুলনা করুন।
2. নিম্ন সূচকে মান বেশি হলে কাউন্টারটি বৃদ্ধি করুন।
3. ফলাফল প্রদর্শন করুন৷
৷উদাহরণ
#include <stdio.h>
int Merge(int arr[], int aux[], int low, int mid, int high) {
int k = low, i = low, j = mid + 1;
int inversionCount = 0;
while (i <= mid && j <= high) {
if (arr[i] <= arr[j]) {
aux[k++] = arr[i++];
} else {
aux[k++] = arr[j++];
inversionCount += (mid - i + 1); // NOTE
}
}
while (i <= mid)
aux[k++] = arr[i++];
for (int i = low; i <= high; i++)
arr[i] = aux[i];
return inversionCount;
}
int MergeSort(int arr[], int aux[], int low, int high) {
if (high == low) // if run size == 1
return 0;
int mid = (low + ((high - low) >> 1));
int inversionCount = 0;
inversionCount += MergeSort(arr, aux, low, mid);
inversionCount += MergeSort(arr, aux, mid + 1, high);
inversionCount += Merge(arr, aux, low, mid, high);
return inversionCount;
}
int main() {
int arr[] = { 1, 9, 6, 4, 5 };
int N = 5;
int aux[N];
for (int i = 0; i < N; i++)
aux[i] = arr[i];
printf("Inversion count is %d", MergeSort(arr, aux, 0, N - 1));
return 0;
} 

