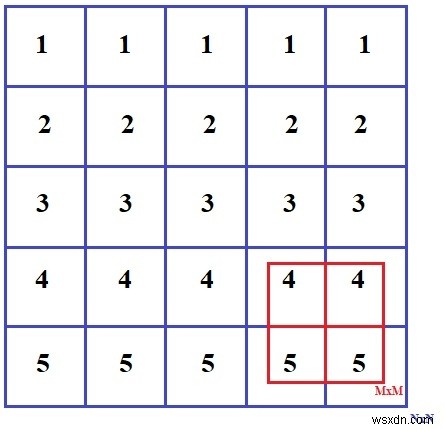
NxN-এর একটি ম্যাট্রিক্স দিলে MxM-এর একটি সাব ম্যাট্রিক্স পাওয়া যায় যেখানে M<=N এবং M>=1 ম্যাট্রিক্স MxM-এর সমস্ত উপাদানের যোগ সর্বাধিক। ম্যাট্রিক্স NxN এর ইনপুটে শূন্য, ধনাত্মক এবং ঋণাত্মক পূর্ণসংখ্যার মান থাকতে পারে।
উদাহরণ
Input:
{{1, 1, 1, 1, 1},
{2, 2, 2, 2, 2},
{3, 3, 3, 3, 3},
{4, 4, 4, 4, 4},
{5, 5, 5, 5, 5} }
Output:
4 4
5 5 উপরের সমস্যাটি একটি সহজ সমাধান দ্বারা সমাধান করা যেতে পারে যেখানে আমরা পুরো ম্যাট্রিক্স NxN নিতে পারি, তারপরে সম্ভাব্য সমস্ত MxM ম্যাট্রিক্স খুঁজে বের করতে পারি এবং তাদের যোগফল খুঁজে বের করতে পারি, তারপর সর্বাধিক যোগফল সহ MxM এর একটি ম্যাট্রিক্স প্রিন্ট করতে পারি। এই পদ্ধতিটি সহজ কিন্তু O(N^2.M^2) সময়ের জটিলতা প্রয়োজন, তাই আমরা এমন একটি উপায় খুঁজে বের করার চেষ্টা করি যাতে কম জটিলতা লাগে।
অ্যালগরিদম
Start
Step 1 -> Declare Function void matrix(int arr[][size], int k)
IF k>size
Return
Declare int array[size][size]
Loop For int j=0 and j<size and j++
Set sum=0
Loop for int i=0 and i<k and i++
Set sum=sum + arr[i][j]
End
Set array[0][j]=sum
Loop For int i=1 and i<size-k+1 and i++
Set sum=sum+(arr[i+k-1]][j]-arr[i-1][j]
Set arrayi][j]=sum
End
Set int maxsum = INT_MIN and *pos = NULL
Loop For int i=0 and i<size-k+1 and i++)
Set int sum = 0
Loop For int j = 0 and j<k and j++
Set sum += array[i][j]
End
If sum > maxsum
Set maxsum = sum
Set pos = &(arr[i][0])
End
Loop For int j=1 and j<size-k+1 and j++
Set sum += (array[i][j+k-1] - array[i][j-1])
IF sum > maxsum
Set maxsum = sum
Set pos = &(arr[i][j])
End
End
End
Loop For int i=0 and i<k and i++
Loop For int j=0 and j<k and j++
Print *(pos + i*size + j)
End
Print \n
End
Step 2 -> In main()
Declare int array[size][size] = {{1, 1, 1, 1, 1}, {2, 2, 2, 2, 2}, {3, 3, 3, 3, 3}, {4, 4, 4, 4, 4}, {5, 5, 5, 5, 5}}
Declare int k = 2
Call matrix(array, k)
Stop উদাহরণ
#include <bits/stdc++.h>
using namespace std;
#define size 5
void matrix(int arr[][size], int k){
if (k > size) return;
int array[size][size];
for (int j=0; j<size; j++){
int sum = 0;
for (int i=0; i<k; i++)
sum += arr[i][j];
array[0][j] = sum;
for (int i=1; i<size-k+1; i++){
sum += (arr[i+k-1][j] - arr[i-1][j]);
array[i][j] = sum;
}
}
int maxsum = INT_MIN, *pos = NULL;
for (int i=0; i<size-k+1; i++){
int sum = 0;
for (int j = 0; j<k; j++)
sum += array[i][j];
if (sum > maxsum){
maxsum = sum;
pos = &(arr[i][0]);
}
for (int j=1; j<size-k+1; j++){
sum += (array[i][j+k-1] - array[i][j-1]);
if (sum > maxsum){
maxsum = sum;
pos = &(arr[i][j]);
}
}
}
for (int i=0; i<k; i++){
for (int j=0; j<k; j++)
cout << *(pos + i*size + j) << " ";
cout << endl;
}
}
int main(){
int array[size][size] = {
{1, 1, 1, 1, 1},
{2, 2, 2, 2, 2},
{3, 3, 3, 3, 3},
{4, 4, 4, 4, 4},
{5, 5, 5, 5, 5},
};
int k = 2;
matrix(array, k);
return 0;
} আউটপুট
যদি আমরা উপরের প্রোগ্রামটি চালাই তবে এটি নিম্নলিখিত আউটপুট তৈরি করবে
4 4 5 5


