N ভগ্নাংশের লব সংখ্যা এবং হর ডেন দেওয়া, কাজ হল পণ্য N ভগ্নাংশ খুঁজে বের করা এবং আউটপুট হ্রাস আকারে হওয়া উচিত।
নীচের চিত্রের মতো আমাদের দুটি ভগ্নাংশ রয়েছে "4/5" এবং "3/4" আমরা সেই দুটি উপদলের গুণফল খুঁজে পেয়েছি যেখানে প্রথমটির লবটি দ্বিতীয়টির লব দ্বারা গুণিত হয় এবং প্রথমটির হরটি গুণিত হয়। দ্বিতীয়টির হর এখন চূড়ান্ত ফলাফল হল “12/20” যা কমানো যেতে পারে তাই আউটপুট হবে “3/5” একইভাবে প্রদত্ত সমস্যা সমাধানের জন্য আমাদের একটি প্রোগ্রাম তৈরি করতে হবে।
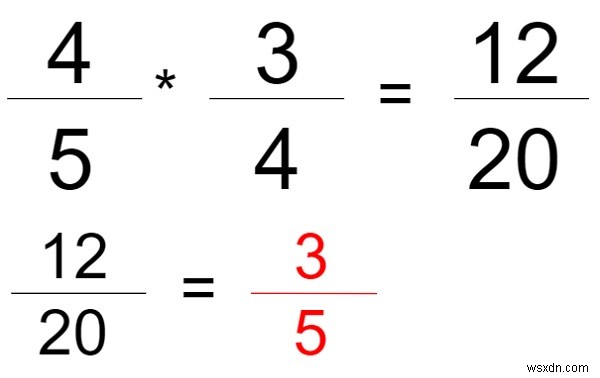
ইনপুট
fraction f[3] = {{1,2},
{2,1},
{5,6}} আউটপুট
5/6
ব্যাখ্যা − 1/2 * 2/1 * 5/6 =10/12 তাই আমরা এটিকে 5/6 হিসাবে কমাতে পারি।
ইনপুট
fraction f[2] = {{2, 3},
{1,4}} আউটপুট
1/6
ব্যাখ্যা − 2/3 * 1/4 =2/12 যা 1/6 হিসাবে হ্রাস করা যেতে পারে
সমস্যা সমাধানের জন্য নিচের পদ্ধতিটি ব্যবহার করা হয়েছে
উপরের সমস্যাটি সমাধান করার জন্য আমরা সমস্ত হর এবং লব গুণতে পারি, ফলাফলটিকে অন্য একটি ভেরিয়েবলে সংরক্ষণ করতে পারি prod_den এবং prod_num যা হবে যথাক্রমে চূড়ান্ত হর এবং চূড়ান্ত লব এখন আমাদের হ্রাসকৃত ফর্মটি খুঁজে বের করতে হবে, এর জন্য আমাদের GCD খুঁজে বের করতে হবে। prod_num এবং prod_den এর (সর্বশ্রেষ্ঠ সাধারণ ভাজক) এবং prod_num এবং prod_den তাদের নিজ নিজ GCD দিয়ে ভাগ করুন।
অ্যালগরিদম
Start
Declare a struct fraction with following elements
1. num, 2. den
In function int GCD(int a, int b)
Step 1→ If a == 0 then,
Return b
Step 2→ Return GCD(b % a, a)
In function int product(int n, fraction f[])
Step 1→ Initialize prod_num = 1 prod_den = 1
Step 2→ Loop For i = 0; i < n; i++
prod_num = prod_num * f[i].num
prod_den = prod_den * f[i].den
Step 3→ Declare and initialize gcd = GCD(prod_num, prod_den)
Step 4→ prod_num = prod_num / gcd
Step 5→ prod_den = prod_den / gcd
Step 6→ Print prod_num, prod_den
In Function int main()
Step 1→ Declare struct fraction f[3] = {
{1,2},
{2,1},
{5,6}}
Step 2→ Declare and initialization n as sizeof(f)/sizeof(f[0])
Step 3→ product(n, f)
Stop হিসাবে উদাহরণ
#include <stdio.h>
struct fraction{
int num;
int den;
};
// Function to return gcd of a and b
int GCD(int a, int b){
if (a == 0)
return b;
return GCD(b % a, a);
}
//fucntion to print the result
int product(int n, fraction f[]){
int prod_num = 1, prod_den = 1;
// finding the product of all N
// numerators and denominators.
for (int i = 0; i < n; i++) {
prod_num *= f[i].num;
prod_den *= f[i].den;
}
// Finding GCD of new numerator and
// denominator
int gcd = GCD(prod_num, prod_den);
// finding reduced form
prod_num /= gcd;
prod_den /= gcd;
printf("%d/%d\n", prod_num, prod_den);
return 0;
}
int main(){
struct fraction f[3] = {
{1,2},
{2,1},
{5,6}};
int n = sizeof(f)/sizeof(f[0]);
product(n, f);
return 0;
} আউটপুট
উপরের কোডটি চালালে এটি নিম্নলিখিত আউটপুট −
উৎপন্ন করবে5/6


